Solución de sistemas de ecuaciones lineales
para resolver o hallar el valor de las variables aplicando el algebra matricial en los sistemas de ecuaciones tenemos varios métodos:
1) Solución Gaussiana.
para este utilizaremos el método de Gauss, con este haremos una reducción a la matriz para así obtener los resultados de las variables. Ejemplo:
tenemos las siguientes ecuaciones:
20X + 30Y = 6000
20X + 10Y = 4800
1) debemos sacar los valores que acompañan las variables y las colocaremos en una matriz, en este caso:
| 20 30 |
| 20 10 |
2) vamos a ampliar esta matriz con los resultados de las ecuaciones y nos quedaría algo así:
| 20 30 : 6000 |
| 20 10 : 4800 |
3) usando el método de Gauss aplicaremos operaciones elementales para conseguir que los valores de la matriz principal lleguen a una matriz identidad y así los valores de la ampliación serán los resultados que estamos buscando, así:
| 20 30 : 6000 |
| 20 10 : 4800 | F1 / 20
| 1 1.5 : 300 |
| 20 10 : 4800| F2 - 20 F1
| 1 1.5 : 300 |
| 0 - 20 : - 1200| F2 / -20
| 1 1.5 : 300 |
| 0 1 : 60 | F1 - 1.5 F2
| 1 0 : 210 |
| 0 1 : 60 |
4) de esta manera obtenemos que X tiene como valor 210 y Y tiene como valor 60, para comprobar cambiamos estos valores en las ecuaciones y comprobamos si dan los resultados que debe, así:
20X + 30Y = 6000 // 20 . (210) + 30 . (60) = 6000
20X + 10Y = 4800 // 20 . (210) + 10 . (60) = 4800
5) una vez comprobamos ya tendríamos el resultado
X = 210
Y = 60
2) Solución por determinantes.
En este método tendremos que tener en cuenta la siguiente formula llamada reglas de Cramer:
X = DX / D
donde X puede ser cualquier variable, DX es el determinante despejando esta variable y D es el determinante de la matriz realizada con las ecuaciones, para despejar la formula hacemos los siguientes pasos:
1) tenemos las mismas ecuaciones
20X + 30Y = 6000
20X + 10Y = 4800
2) hacemos una matriz con los valores que acompañan las variables:
| 20 30 |
| 20 10 |
3) hallamos el determinante de esta matriz:
( 20 x 10 ) - ( 30 x 20 ) = - 400 // esto seria D
4) ahora vamos a intercambiar los valores de X en la matriz por los resultados de las ecuaciones y de nuevo hallamos el determinante, así:
| 6000 30 |
| 4800 10 |
( 6000 x 10 ) - ( 30 x 4800 ) = - 84.000 // esto seria DX
5) repetimos este intercambio las veces que sean necesarios, es decir, si tenemos 3 variables intercambiamos las 3 variables y hallamos el determinante en este caso tenemos 2 variables por lo que solo lo vamos a repetir una vez mas, así:
| 20 6000 |
| 20 4800 |
( 20 x 4800 ) - ( 6000 x 20 ) = - 24.000 // esto seria DY
6) ahora teniendo estos resultados podemos despejar las formulas de la regla de Cramer las cuales serian:
X = DX / D
Y = DY / D
X = - 84.000 / -400
X = 210
Y = - 24.000 / -400
Y = 60
7) una vez obtenemos estos resultados podemos comprobar de nuevo con las ecuaciones
20X + 30Y = 6000 // 20 . (210) + 30 . (60) = 6000
20X + 10Y = 4800 // 20 . (210) + 10 . (60) = 4800
8) una vez comprobamos ya tendríamos el resultado
X = 210
Y = 60
3) Solución por plano cartesiano.
Para usar este método debemos hacer lo siguiente:
tenemos las siguientes ecuaciones:
20X + 30Y = 6000
20X + 10Y = 4800
1) debemos sacar las variables como si tuviéramos una tabla la cual las columnas representan a cada una y debajo tenemos sus valores, es decir
X Y
0 0
0 0
2) en un principio no tenemos claro su valor por lo que debemos hacer lo siguiente, dejaremos una de las 2 variables en 0 y hallaremos un numero que al aplicarlo en la otra variable nos de el resultado de las ecuaciones, es decir:
primero dejamos la X en 0, luego hallamos un numero que al aplicarlo en Y y al usar la ecuación numero 1 esta se cumpla
X Y 20 . (0) + 30 . (?) = 6000
0 0
0 0
en este caso nos conviene que Y valga 200
X Y 20 . (0) + 30 . (?) = 6000
0 200
0 0
ahora hacemos lo mismo pero dejando Y en 0 y hallando un valor para X
X Y 20 . (?) + 30 . (0) = 6000
0 200
0 0
como podemos comprobar en este caso conviene que X valga 300
X Y 20 . (300) + 30 . (0) = 6000
0 200
300 0
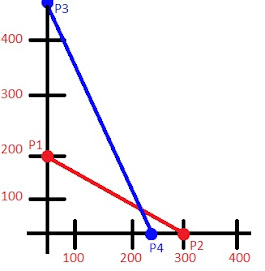
ahora esto lo podemos graficar en un plano cartesiano de la siguiente manera
P1 = ( 0 , 200 )
P2 = ( 300 , 0 )
3) esto lo hemos hecho con la primera ecuación ahora debemos hacer lo mismo con la segunda de la misma manera.
primero dejamos la X en 0, luego hallamos un numero que al aplicarlo en Y y al usar la ecuación numero 2 esta se cumpla
X Y 20 . (0) + 10 . (?) = 4800
0 0
0 0
en este caso nos conviene que Y valga 480
X Y 20 . (0) + 10 . (480) = 4800
0 480
0 0
ahora hacemos lo mismo pero dejando Y en 0 y hallando un valor para X
X Y 20 . (?) + 10 . (0) = 4800
0 480
0 0
como podemos comprobar en este caso conviene que X valga 240
X Y 20 . (240) + 10 . (?) = 4800
0 480
240 0
ahora esto lo podemos graficar en un plano cartesiano de la siguiente manera
P3 = ( 0 , 480 )
P4 = ( 240 , 0 )
4) Por ultimo el punto donde se cruzan las líneas seria nuestro resultado buscado.
en este caso damos con que el resultado seria el antes encontrado ( 210 , 60 )
X = 210
Y = 60
5) una vez obtenemos estos resultados podemos comprobar de nuevo con las ecuaciones
20X + 30Y = 6000 // 20 . (210) + 30 . (60) = 6000
20X + 10Y = 4800 // 20 . (210) + 10 . (60) = 4800
6) una vez comprobamos ya tendríamos el resultado
X = 210
Y = 60



Comentarios
Publicar un comentario